Graphen: die Grundlagen
Die Koordinaten eines Punktes
Die Steigung einer Geraden
Geradengleichungen mit einer Konstante
Geradengleichungen
Andere Formen von Geradengleichungen
Systeme von Geradengleichungen
Andere Formen von Geradengleichungen

Wie wird diese Gleichungsform einer Geraden genannt: ?
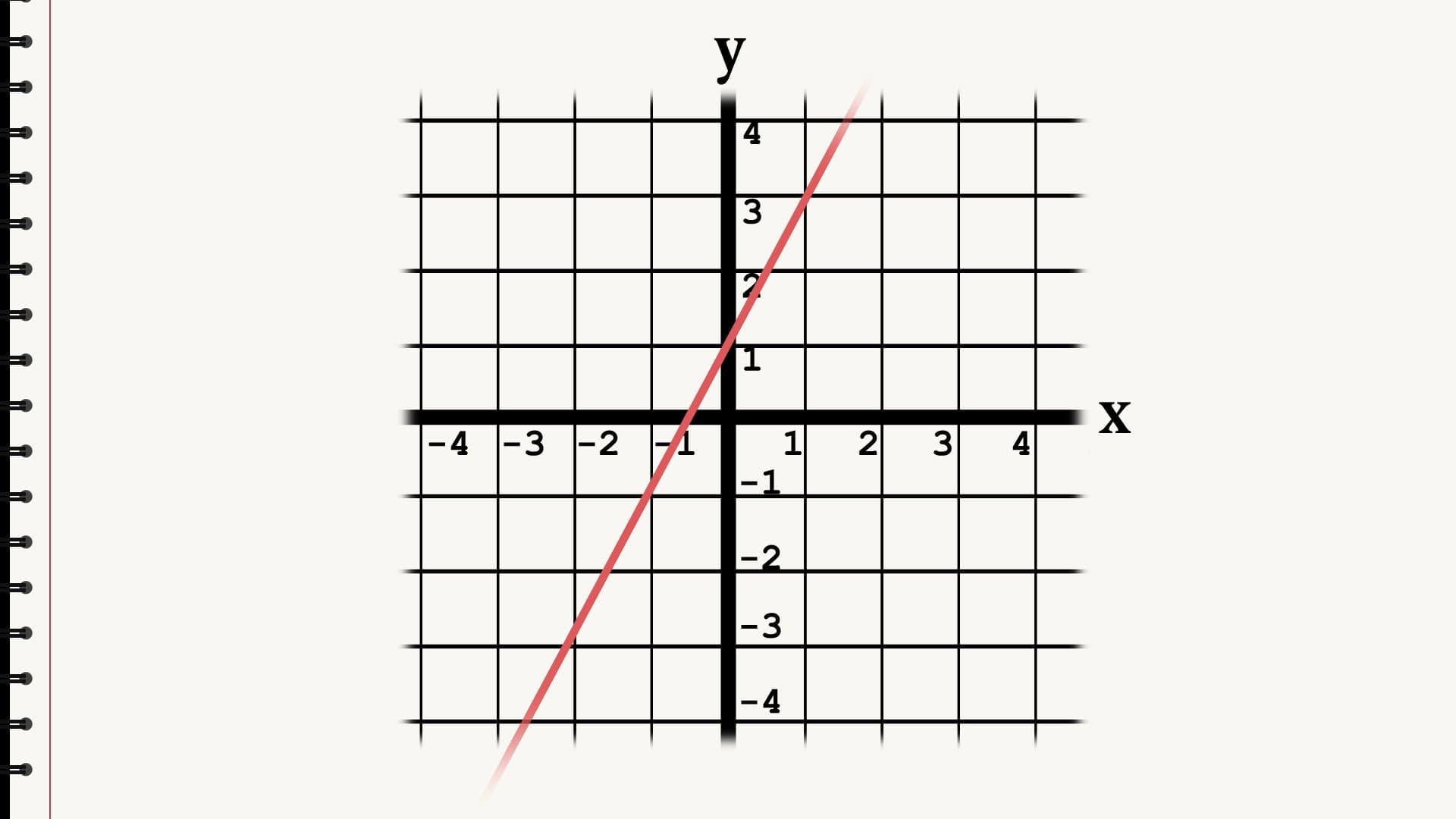
Eine Geradengleichung gibt dir alle Informationen, die du brauchst, um in einem Koordinatensystem eine gerade Linie zu ziehen. Dies ist die häufigste Form der Geradengleichung: Sie wird auch Steigungs- abschnittsform genannt. m ist der Gradient, der die Steigung darstellt. b ist die Konstante, die uns zeigt, wo die Gerade die y-Achse schneidet. Die Geradengleichung kann aber auf verschiedene Weisen geschrieben werden.
Sie kann so aussehen. Oder so. Oder so. Oder auch so. Die ersten drei beschreiben dieselbe Gerade.
Die vierte Form ist etwas Besonderes. Schauen wir sie uns eine nach der anderen an. Hier ist eine Geradengleichung in der Punktsteigungsform. Sie funktioniert so: Wenn du einen Punkt und die Steigung der Geraden kennst, setzt du anstelle von x1 und y1 die x- und y-Koordinate des Punktes in die Gleichung ein. x und y ohne Indizes sind jetzt die zwei Unbekannten in der Gleichung.
Setze für m die Steigung ein, in diesem Fall 2. Löse dann die Gleichung, indem du y auf der linken Seite isolierst, und du erhältst wieder die Gerade in ihrer üblichen Steigungsabschnittsform. Was ist dann mit dieser Form? Diese Form der Geradengleichung nennt man Allgemeine Form. In der Grundform sieht sie so aus.
Beachte, dass c hier nicht den y-Achsenabschnitt anzeigt. Keine Panik, wenn eine lineare Gleichung in dieser Form auftritt. Löse die Gleichung einfach nach y auf – isoliere also y auf der linken Seite – und du bekommst die Steigungsabschnittsform zurück, die du gewöhnt bist. Diese hier ist die einfachste von allen. Die linke Seite liest man als f von x.
Das ist nur eine andere Art zu sagen, dass die Gleichung eine Funktion von x ist. Mit anderen Worten, dass sich etwas verändert, weil sich x verändert. Ansonsten funktioniert sie genauso wie die Steigungsabschnittsform. In diesem Fall wird anstelle von b ein u verwendet, aber es bedeutet dasselbe. Die Buchstaben sind nur Platzhalter, und so lange du die Bedeutung kennst, kannst du jeden beliebigen Buchstaben verwenden.
Zum Beispiel g von t = 2t + a... oder du könntest sogar griechische Buchstaben verwenden, Alpha = 2 Beta + Gamma. Sie haben die gleiche Form und beschreiben die gleiche Gerade. Diese hier ist jedoch anders. Auch das ist eine lineare Gleichung, sie sieht jedoch anders aus.
Sie hat überhaupt keinen y-Wert. Es ist einfach eine Gerade, in der x immer gleich 4 ist, y aber unbestimmt ist. Wie sieht eine solche Gerade aus? Genau, es ist eine gerade vertikale Linie, die parallel zur y-Achse verläuft und die X-Achse bei 4 schneidet. x entspricht auf jedem Punkt dieser Linie 4.
Es gibt kein y, daher ist es nicht definiert. Noch eine. Kannst du dir vorstellen, wie diese Gerade aussieht? y ist hier immer -2 und x ist nicht definiert. Die Gerade sieht so aus: Wenn du dich mit diesen Formen vertraut machst, kannst du immer eine Gerade ins Koordinatensystem zeichnen, egal in welcher Form die Gleichung geschrieben ist.