Gráficos: iniciación
Las coordenadas de un punto
La pendiente de una recta
Ecuación lineal con un término constante
Las ecuaciones lineales
Otros tipos de ecuaciones lineales
Sistemas de ecuaciones lineales
Otros tipos de ecuaciones lineales
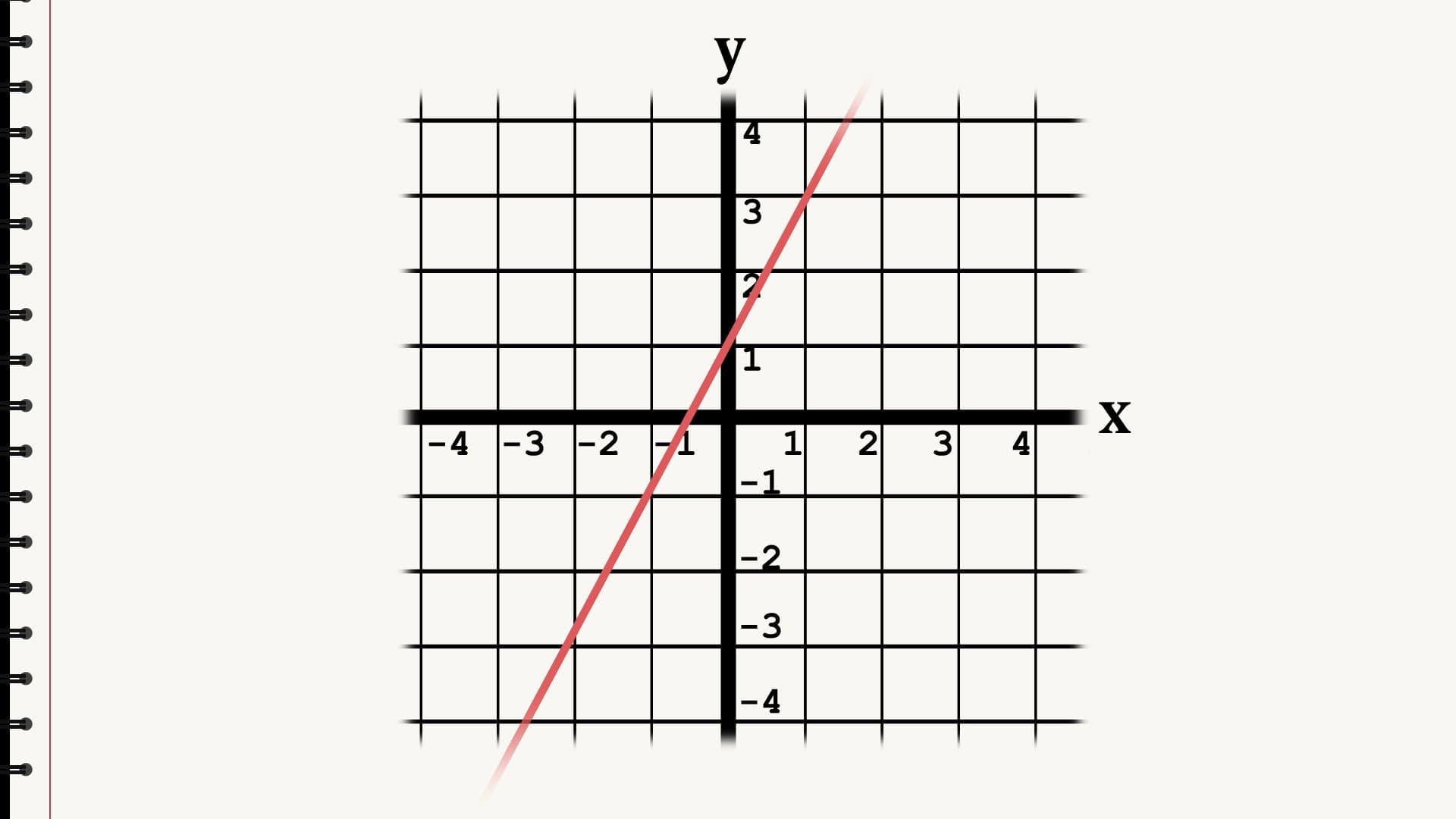

¿Cómo se llama este tipo de ecuación para una recta: ?
La ecuación de una recta nos proporciona toda la información que necesitamos para trazar dicha recta en un sistema de coordenadas. La ecuación de la recta más común es ésta, llamada función afín o pendiente intercepción. K es la inclinación de la pendiente. M es la constante que nos indica el punto por el que pasa la recta por el eje Y. Pero hay otras maneras de escribir la ecuación de una recta.
Así, o así, o así, o así. Las tres primeras describen la misma recta. La cuarta es un poco más especial. Vayamos de una en una. Ésta es la ecuación de una recta en su forma de función afín. Funciona así.
Si conocemos un punto y la pendiente de la recta, cambiamos la X1 y la Y1 de la ecuación por las coordenadas X e Y. Mantenemos la X y la Y sin índices como dos incógnitas en la ecuación. Sustituimos la K de la pendiente, que en este caso es dos, y resolvemos la ecuación aislando la Y en el lado izquierdo. Ya volvemos a tener una recta en su forma afín, ¿Y qué pasa con esta ecuación? A la ecuación de esta recta se la llama forma estándar.
En su forma generalizada se escribe así. Ten presente que la C no nos indica el interceptor de Y. Si te topas con una ecuación lineal con este aspecto, tranquilo. Lo único que tienes que hacer es resolver Y. Es decir, aislar la Y a la izquierda para así volver a la función afín a la que ya estamos acostumbrados. Ésta es la más fácil de todas.
La izquierda se lee como F de X, que simplemente es otra manera de decir que la ecuación es una función de X. En otras palabras, que algo cambia porque X cambia. Funciona exactamente igual que la función afín. Solo que en este caso se ha usado una U en vez de una M, pero el significado es el mismo. Las letras no son más que etiquetas.
Mientras que tengas claro a qué se refieren, puedes usar cualquier letra. Podría ser g(t) = 2t + a. Incluso podrías usar letras del alfabeto griego: α = 2β + γ. Tienen la misma forma y describen la misma recta. Sin embargo, ésta es distinta.
También aquí se trata de una ecuación lineal, pero con un aspecto diferente. La Y no tiene ningún valor. En esta recta X siempre es igual a cuatro, y no dice nada de Y. ¿Qué aspecto tendría esa recta? Pues eso: es una línea recta y vertical paralela al eje Y que cruza el eje X en el punto cuatro. En cualquier punto de esta recta, X es igual a cuatro.
La Y no existe y por lo tanto es indefinida. ¿Sabes cuál es la ecuación de esta recta? En ésta la Y siempre es -2 y la X es indefinida. Se escribe así. Si te familiarizas con estas ecuaciones, siempre podrás trazar una recta en un sistema de coordenadas, independientemente de cómo esté escrita su ecuación.