Grafer och koordinatsystem
Punktens koordinater
Linjens lutning
Konstanten m
Räta linjens graf
Andra former för räta linjens ekvation
Ekvationssystem med räta linjer
Andra former för räta linjens ekvation
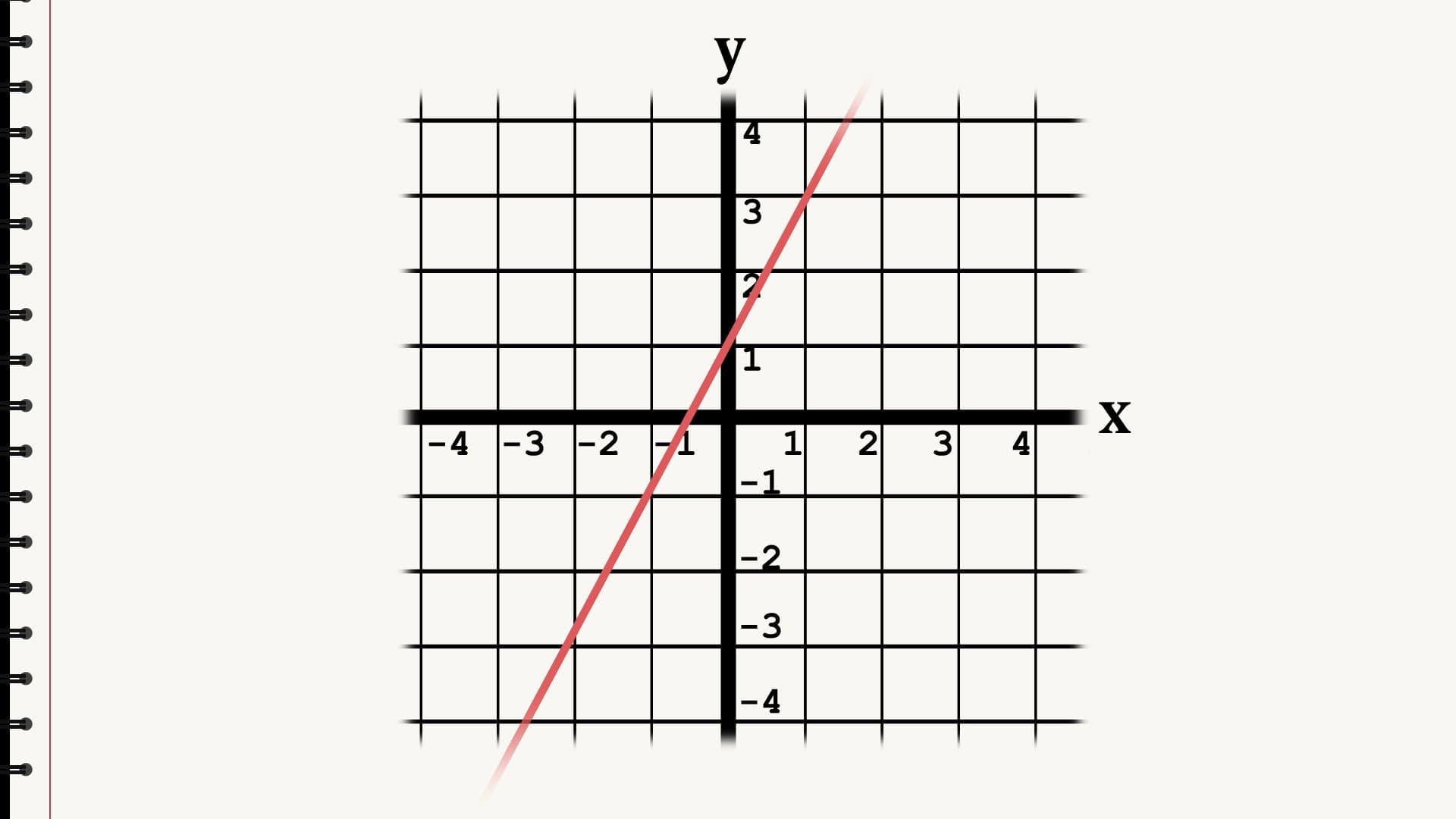

Vad kallas denna form av räta linjens ekvation?
Den räta linjens ekvation ger dig all information du behöver för att rita en rät linje genom ett koordinatsystem. Den vanligaste formen att skriva den räta linjens ekvation är den här. Den kallas k-formen. k är riktningskoefficienten, som anger lutningen. m är konstanttermen, som anger var linjen skär Y-axeln.
Men räta linjen kan skrivas på flera sätt. Den kan se ut så här. Eller så här. Eller så här. Eller så här.
De första tre beskriver samma linje. Den fjärde är lite speciell. Vi tar dem en i taget. Här är den räta linjens ekvation i enpunktsform. Den fungerar så här: Om du känner till en punkt och lutningen på linjen, så byter du ut x och y från den punkten där det står "x1" och "y1" i formeln.
Det x och y som står utan nedsänkta siffror låter du vara kvar, som de två okända i ekvationen. Byt ut k mot lutningen, 2 i det här fallet. Lös ekvationen genom att isolera y i vänsterledet och vips, så har du den räta linjen i sin vanliga k-form igen. Den här varianten då? Det här sättet att skriva räta linjens ekvation kallas för allmän form.
Skriver vi den utan värden på variablerna ser den ut så här. Märk att C här inte säger var linjen skär Y-axeln. Om du möter en linjär funktion i det här formatet, så bli inte rädd. Lös bara ekvationen med avseende på y, det vill säga isolera y i vänsterledet och du får tillbaka k-formen som du är van vid. Det här är den enklaste av alla.
Vänsterledet läser du ut som "f av x". Det är bara ett annat sätt att skriva, för att klargöra att ekvationen är en funktion av x. Alltså att något ändras som ett resultat av att x förändras. Annars fungerar det exakt som k-formen. I det här fallet används u istället för m, men det betyder samma sak.
Bokstäverna är bara etiketter och så länge du vet vad de betyder, kan du använda vilken bokstav som helst. Det kan vara g av t är lika med 2t plus a, eller till och med på grekiska: alfa är lika med två beta plus gamma. De har samma form och alla beskriver samma linje. Den här däremot, är annorlunda. Det är också en linjär ekvation, men den ser annorlunda ut.
Den har inget k-värde alls. Det här är en linje där x alltid är lika med fyra, och som inte säger något alls om y. Hur kan en sån linje se ut? Jo, det är en rak vertikal linje, parallell med Y-axeln, och som korsar X-axeln vid 4. Vid varje punkt på den här linjen är x lika med 4.
y lämnas utanför och är odefinierat. Den här då, kan du gissa hur den här linjen skrivs som en linjär funktion? Här är y alltid -2, och x är odefinierat. Så den ritas så här. Om du bekantar dig med de här formaten så kan du alltid rita ut en linje i ett koordinatsystem, oavsett vilket format ekvationen är skriven i.